偏差値のお話 2008.11.8.更新
偏差値(へんさち)とは?
入試シーズンになると、よく「偏差値」という言葉を耳にします。志望校の難易度や受験生の合格可能性を考える時に無くてはならないものになった「偏差値」。では、この「偏差値」はきちんと理解されて活用されているのでしょうか?
「偏差値」とは、数学の1分野である統計学で用いられているものです。ある数値が、全体の平均からどれくらいズレているかを表す数値であり、これによって、例えばテストが難しくても易しくても、そのでき具合を簡単に比較することができる便利なものです。偏差値は下の式で求められます。
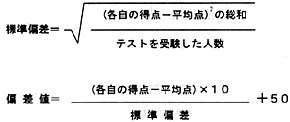
ここでいう「標準偏差」とは、ばらつきを示す数値です。例えば、平均点を中心にして0点から100点まで万遍なく得点が分布すると「標準偏差」は大きくなり、逆に得点差が小さいと「標準偏差」は小さくなります。どちらにしても、テストのでき不できは得点だけではうまくはかることができません。数点の違いで順位が大きく変わることもあるからです。そこで登場したのが「偏差値」なのです。ばらつきの違いは「標準偏差」が吸収してくれるので、「標準偏差」から求まる「偏差値」は、テストのでき不できを考えるのにとても便利なのです。
「偏差値」は、自分の得点が平均点と同じ時、自分の偏差値は必ず50.0となります。平均点より低得点の時は50.0より小さく、平均点より高得点の時は50.0よりも大きな偏差値となります(下の表)。
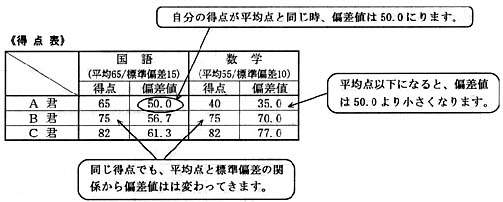
偏差値は、
*問題の難易度にかかわらず、全受験者中の自分の位置を客観的に知ることができる *時期の違うテストでも自分の学力レベルを正確に知ることができるので、 学力の変化を正確につかむことができる
という特徴を持つのです。しかし、注意も必要です。
偏差値は、全体の受験者の中の自分の(相対的な)位置を示すものです。受験者のレベルで偏差値そのものは大きく変わります。受験者のレベルが高い模擬試験では、自分の偏差値が低くでることがあります。だから、Aという模擬試験の自分の偏差値を使って、Bという模擬試験の志望校の合格可能性を判定することには全く意味がありません。
また、注意すべきことは、テストの得点(素点)と偏差値は全然違うものだということです。例えば10の違いをみてみましょう。テストの得点の60点と70点とでは実力の違いがそれほど大きいとは言えません。が、偏差値60と偏差値70とでは、1000人のテストだとすれば、
偏差値50 偏差値60 偏差値70 偏差値80 トップから
50% およそ16% およそ2% およそ0.1%
このようになるので、偏差値60では1000人中160番目、偏差値70では1000人中20番目の成績となります。つまり、偏差値10の違いは、得点10の違いよりも大きな実力差を示しているのです。
偏差値を上手に活用して、学習に役立てたいものですね。
トップページへ